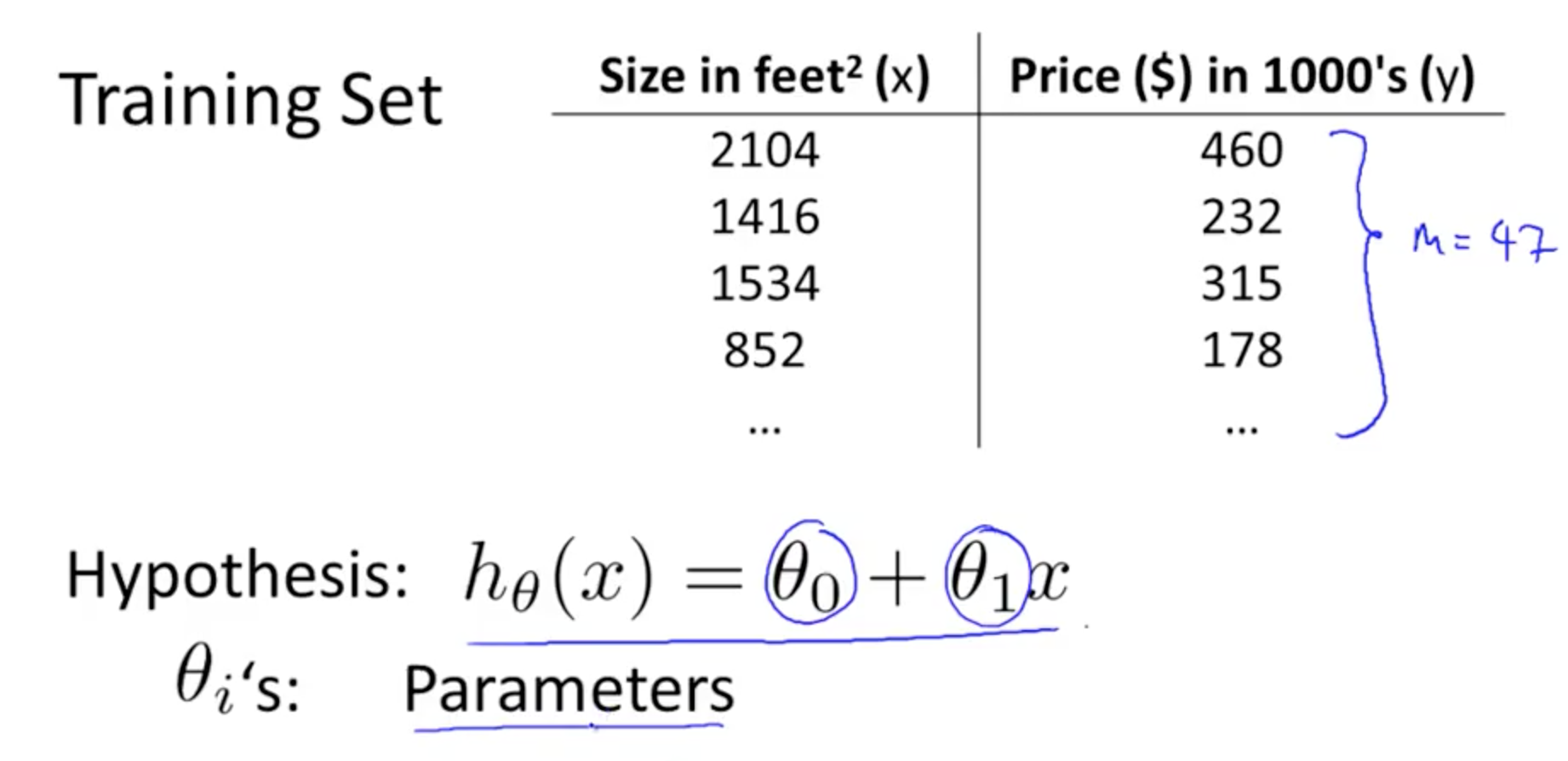
如上所示,给定一个训练集,假设数据拟合的模型结构为一元线性结构,我们需要解决的问题是如何根据数据集,求解出合适的参数值。不同的参数值决定了拟合直线的走向。
当我们求解出了参数值,对模型进行了拟合后,需要评价模型预测的精度如何,需要一个对模型的评价标准,代价函数便是做这样的工作。
在线性回归问题中,常用的代价函数是方差平方和(也叫最小二乘法)。使用预测值与真实值差值的平房和来对模型的精度进行评价。
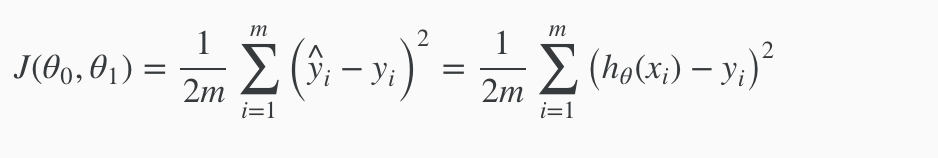
最合理的参数值应当使代价函数的值最小,由此参数的求解问题,转化到数学求极值问题。

而代价函数的极值问题,不同的函数其极值的分布可能是复杂的,比较简单的二次函数的代价函数模型可能如下:
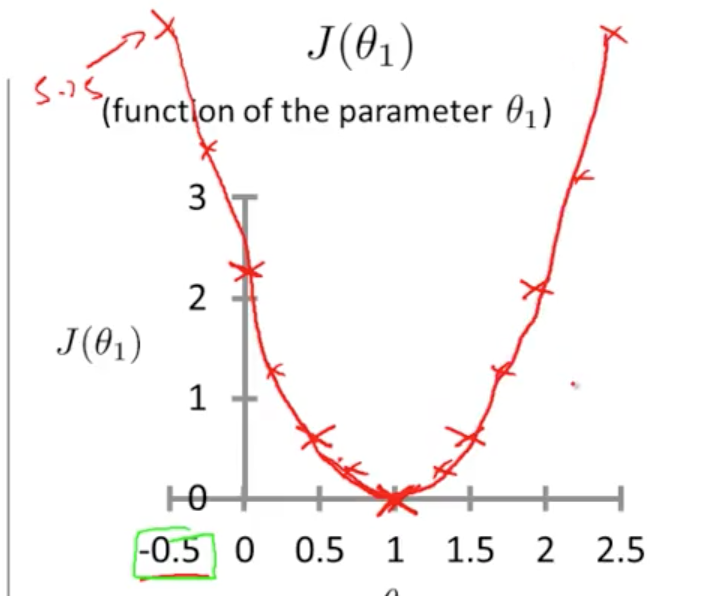
显然当参数值取1的时候函数取最小值,由此确定参数值
假设现在需要求的参数值有两个,那么最后的图可能是这样的:
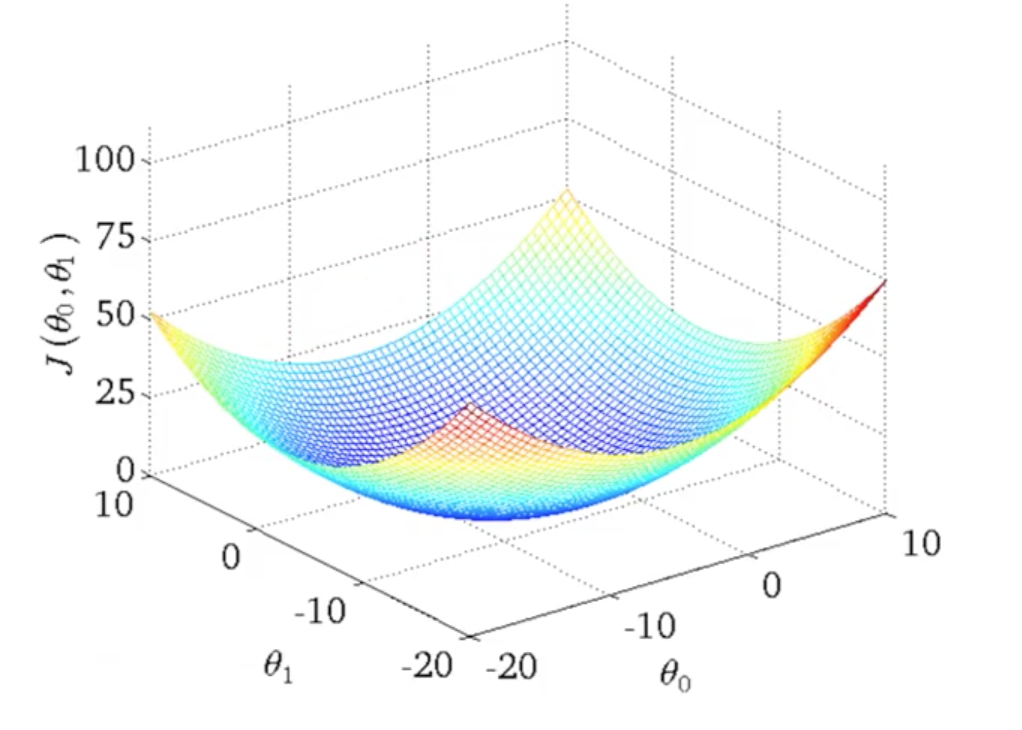
我们去掉J轴,用地理学中等高线的概念的表示上面的三维图,等高线的高度从外圈向内圈递减,同一条线的上J轴值相等如下右图所示:
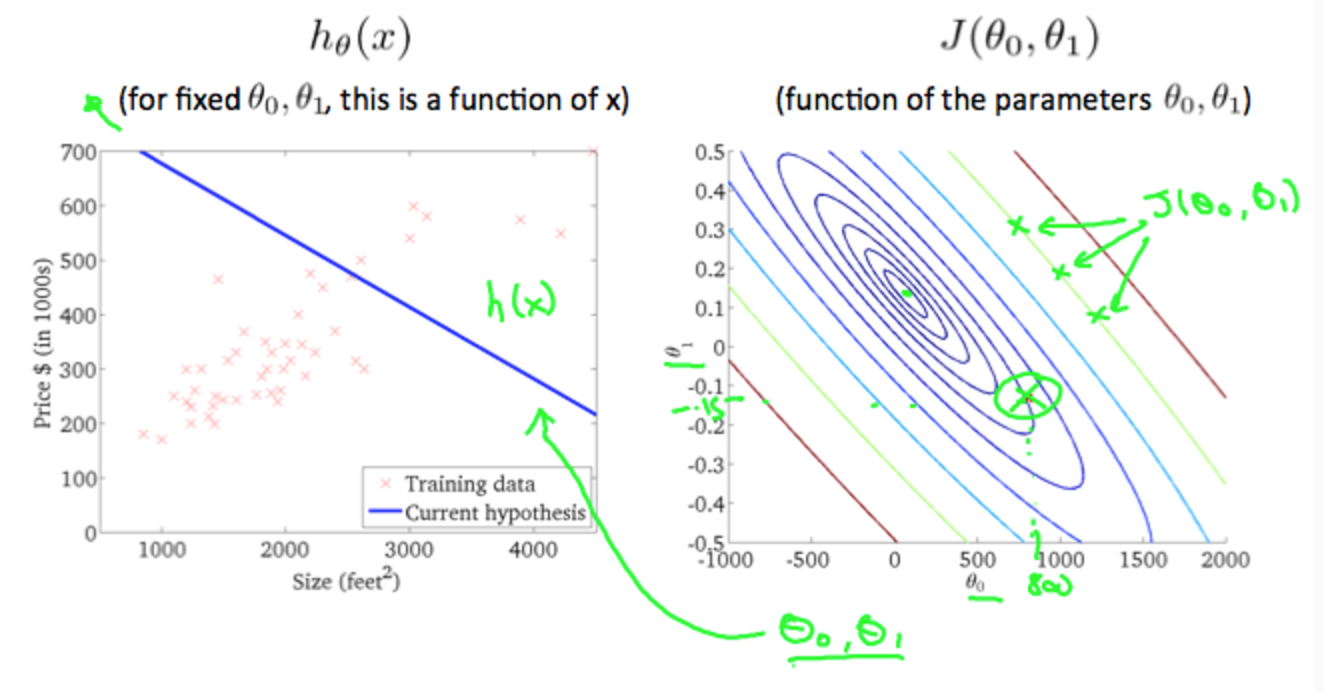
在这两个参数所建立的二维坐标系中,每确定一组参数值,将有对应的J轴值,由图可知,J轴的最小值是最小圆的中心点。。
对于更多为的参数,我们无法画出这样的图形进行人工筛选求解,会通过梯段算法或者牛顿方法进行求解