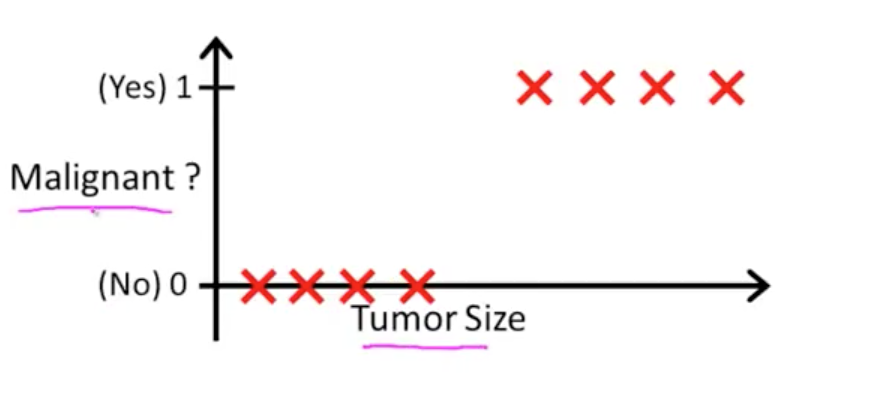
一个这样的例子:0表示没有得肿瘤 1表示得了恶性肿瘤,在二维坐标系上建立关系,横轴表示肿瘤大小,纵轴代表是否得了恶性肿瘤。
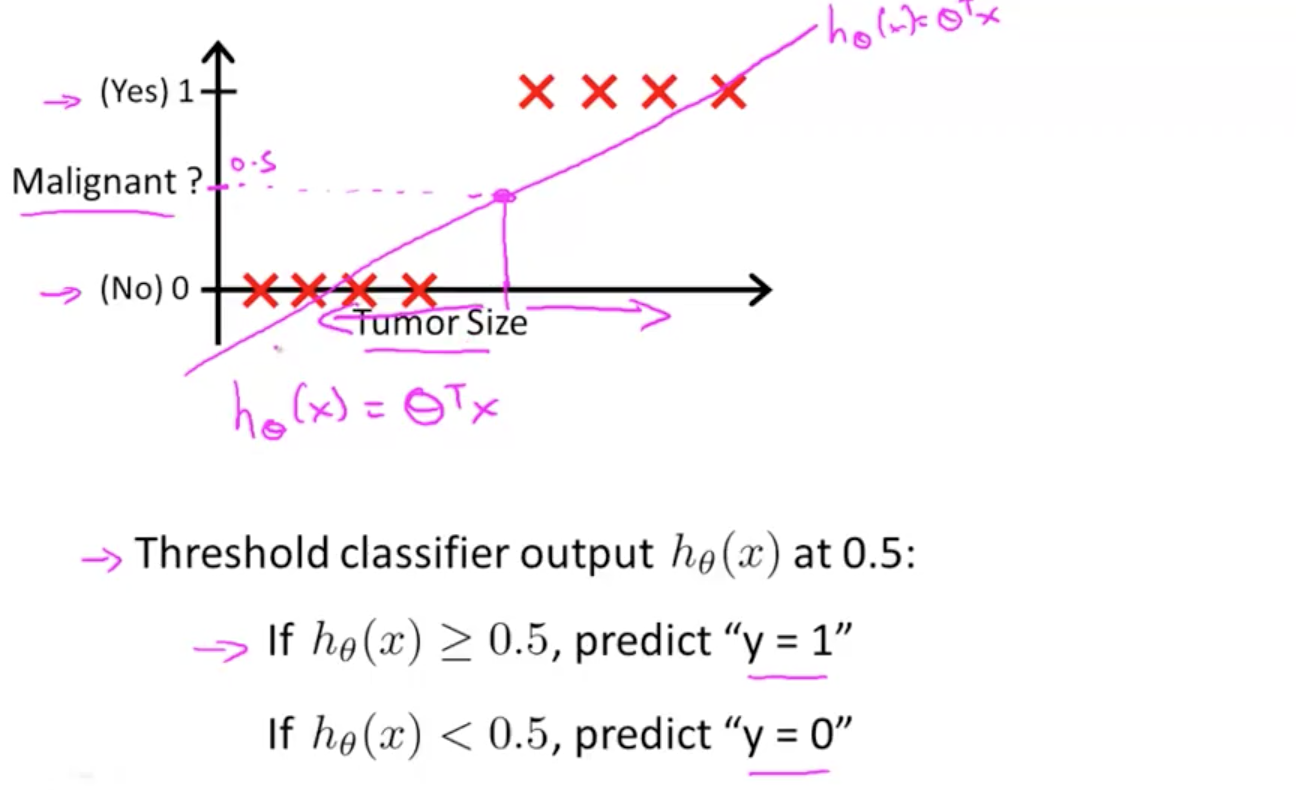
我们画一条线去拟合这些点,设置一个阈值,比如0.5,函数输出值大于0.5归类1 ,函数小于0.5归类0。

当我们仅仅用线性回归去拟合,线性回归的的取值域往往不在[0,1]之间,这显然是不合理的。
下面引出logistic线性回归,解决二分类问题。
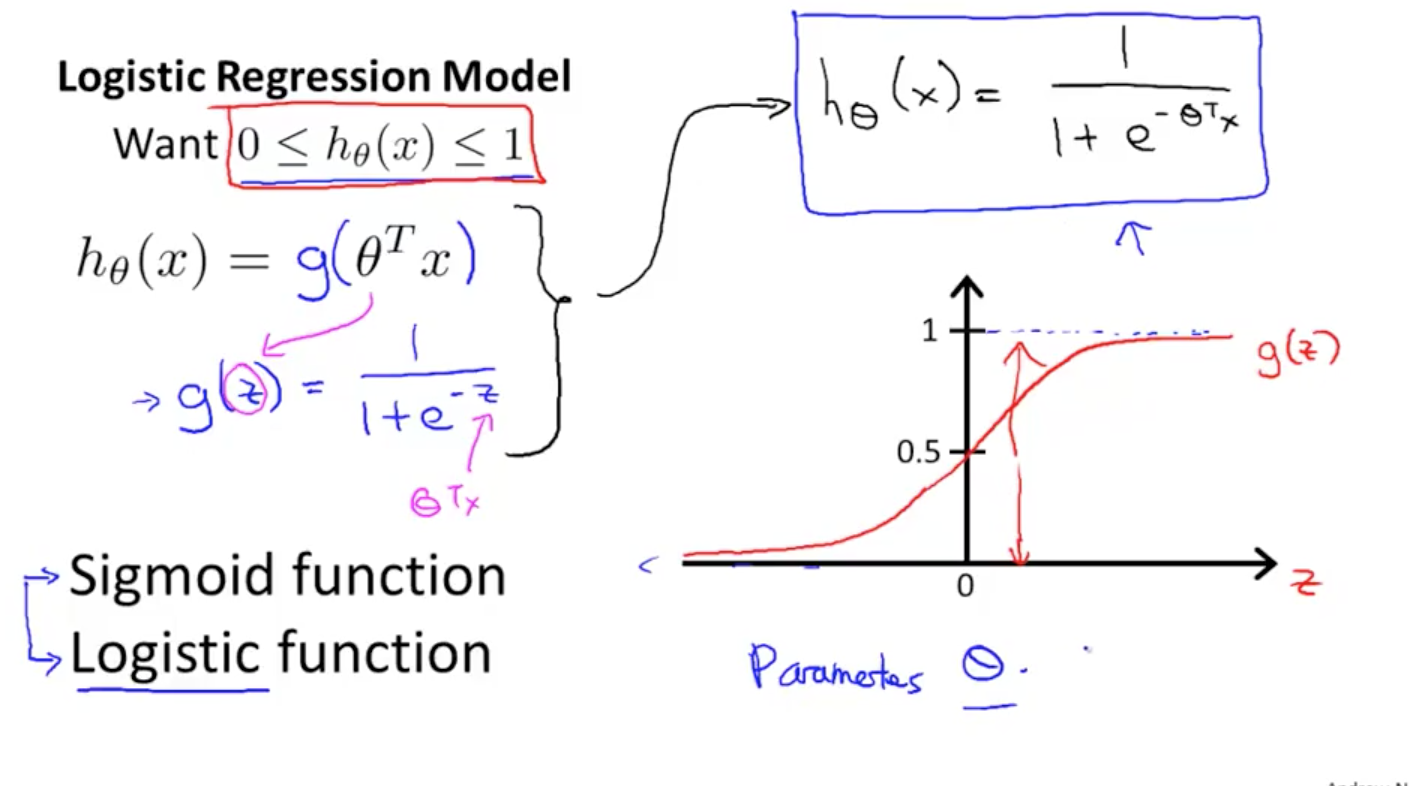
上面说到,我们希望函数的输出在0与1之间,logistic线性函数即满足这种特征,logistic函数解决了输出值必须在0,1内的问题,但是划分边界需要假设函数(决策边界)自己去定义。
hθ(x)=g(θTx)
z=θTx
g(z)=11+e−z
我们预测一个病人得了恶性肿瘤的概率
P(y=1|x;theTa) 读作在给定x,参数为theTa的情况下,得了恶性肿瘤的概率。
决策边界

假设函数为
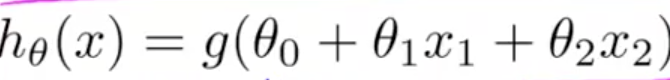
有图可知,要是y = 1 ,那么g(z)必须大于或等于0.5 ,此时,z>0,即h(x)>=0
假设参数已经知道,分别 -3 ,1,1,那么假设函数为
h(x) = -3 + x1 + x2;
-3+x1+x2 >=0

那么这条线成为决策边界,那么h(x)=0实际上就是决策边界。但是并非所有情况下,决策边界都是线性的。

如图所示,决策边界应当是个圆形,那么我我们可以使用多项式的方式去拟合这个边界。
逻辑回归的代价函数
我们不能直接使用最小二乘法作为逻辑回归的代价函数,因为将函数带入后会发现,代价函数是非凸函数,这给求极值带来了困难。因为h(x)的值域为[0,1]
我们使用去log的方式代替
J(θ)=1m∑i=1mCost(hθ(x(i)),y(i))
Cost(hθ(x),y)=−log(hθ(x)) if y = 1
Cost(hθ(x),y)=−log(1−hθ(x)) if y = 0
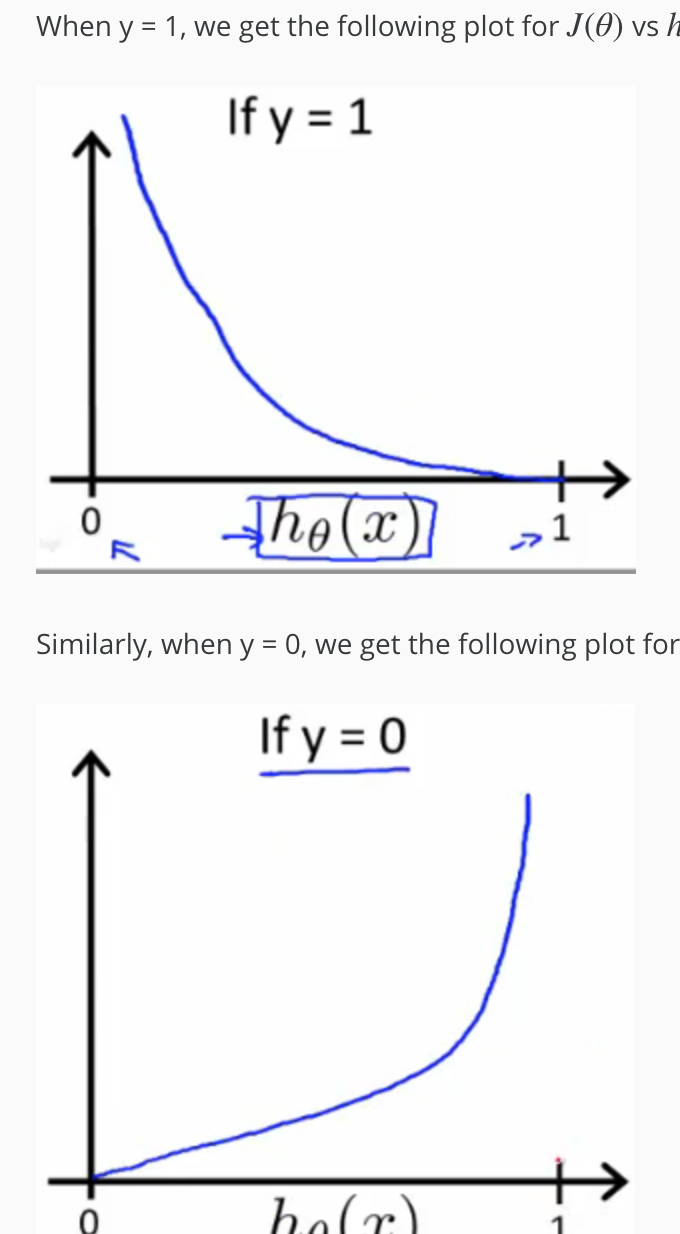
通过变换代价函数为等方向的凸,使得求极值跟容易。