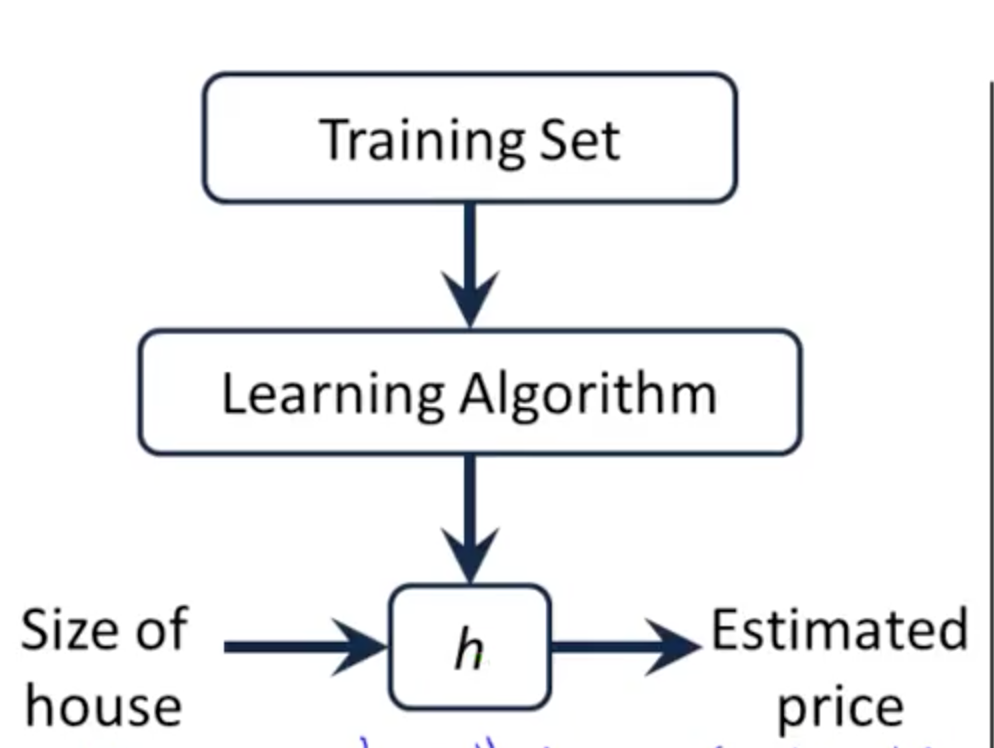
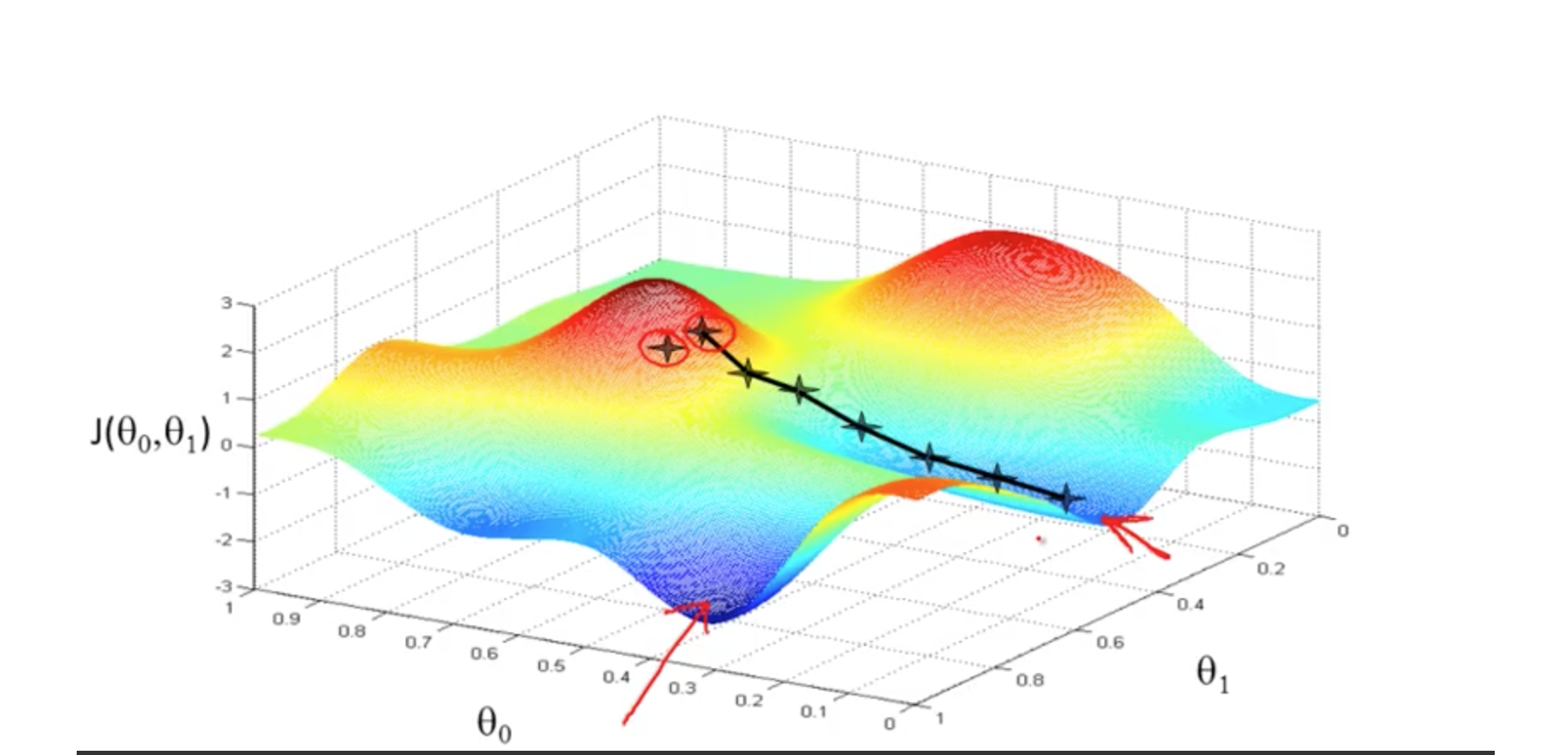
求代价函数最小值问题，如果是正规方程，我们可以对每个参数值求导并令导数为0。
我们队最小二乘法进行参数求导，最终得到的关系如上图所示
如果使用了正规方程，那么就不需要进行特征缩放（特征变量归一化处理，便于进行梯度下降）取相似范围，因为最终算出来的结果是一样的.
我们可以使用matlab或者Octave来进行正规方程的计算。
推荐使用pin函数来进行计算，因为正规方程中设计的矩阵逆运算，即是矩阵没有逆矩阵也会给出结果。
那么是什么导致举证不可逆呢？
存在多余的相似特征，我们可以删除他
太多的特征导致行数小于列数，我们可以通过删减特征以使举证为方阵，矩阵的可逆是建立在方阵基础上的
特征缩放一般希望将特征值缩放到-1 到 1之间或者非常相近的区域之间，这样做的原因是为了便于梯度下降算法运行的更快。
只要缩放到相近似的范围即可
如图缩放的方式为：
（x-u)/s ,其中x是特征值，u是均值，s是值范围。
如何确定梯度下降运行正确？
如何确定学习速率？
由梯度下降公式可知，学习速率越大，j函数值下降的越快，越快速趋缓，在较少的迭代中，函数值迅速趋向缓和表明学习速率大
如果学习速率太小，收敛速度慢，如果学习速率太大，可能会错过收敛点
为了确定学习速率多少合适，可以先设定一个学习速率，迭代几次值，画出二维坐标，连线看先下降的趋势，如上图，通过下降趋势来判断设置的学习速率是偏大还是偏小
面对一个事物，我们选取什么特征进行建模需要多方考虑，有时候需要将多个特征综合起来表示成一个特征，比如房子的宽高我们可以表示为面积
一个这样的例子：0表示没有得肿瘤 1表示得了恶性肿瘤，在二维坐标系上建立关系，横轴表示肿瘤大小，纵轴代表是否得了恶性肿瘤。
我们画一条线去拟合这些点，设置一个阈值，比如0.5，函数输出值大于0.5归类1 ，函数小于0.5归类0。
当我们仅仅用线性回归去拟合，线性回归的的取值域往往不在[0,1]之间，这显然是不合理的。
下面引出logistic线性回归，解决二分类问题。
上面说到，我们希望函数的输出在0与1之间，logistic线性函数即满足这种特征，logistic函数解决了输出值必须在0，1内的问题，但是划分边界需要假设函数（决策边界）自己去定义。
hθ(x)=g(θTx)
z=θTx
g(z)=11+e−z
我们预测一个病人得了恶性肿瘤的概率
P(y=1|x;theTa) 读作在给定x，参数为theTa的情况下，得了恶性肿瘤的概率。
决策边界
假设函数为
有图可知，要是y = 1 ，那么g(z)必须大于或等于0.5 ，此时,z>0,即h(x)>=0
假设参数已经知道，分别 -3 ，1，1，那么假设函数为
h(x) = -3 + x1 + x2;
-3+x1+x2 >=0
那么这条线成为决策边界，那么h(x)=0实际上就是决策边界。但是并非所有情况下，决策边界都是线性的。
如图所示，决策边界应当是个圆形，那么我我们可以使用多项式的方式去拟合这个边界。
逻辑回归的代价函数
我们不能直接使用最小二乘法作为逻辑回归的代价函数，因为将函数带入后会发现，代价函数是非凸函数，这给求极值带来了困难。因为h(x)的值域为[0,1]
我们使用去log的方式代替
J(θ)=1m∑i=1mCost(hθ(x(i)),y(i))
Cost(hθ(x),y)=−log(hθ(x)) if y = 1
Cost(hθ(x),y)=−log(1−hθ(x)) if y = 0
通过变换代价函数为等方向的凸，使得求极值跟容易。
如上所示，给定一个训练集，假设数据拟合的模型结构为一元线性结构，我们需要解决的问题是如何根据数据集，求解出合适的参数值。不同的参数值决定了拟合直线的走向。
当我们求解出了参数值，对模型进行了拟合后，需要评价模型预测的精度如何，需要一个对模型的评价标准，代价函数便是做这样的工作。
在线性回归问题中，常用的代价函数是方差平方和（也叫最小二乘法）。使用预测值与真实值差值的平房和来对模型的精度进行评价。
最合理的参数值应当使代价函数的值最小，由此参数的求解问题，转化到数学求极值问题。
而代价函数的极值问题，不同的函数其极值的分布可能是复杂的，比较简单的二次函数的代价函数模型可能如下：
显然当参数值取1的时候函数取最小值，由此确定参数值
假设现在需要求的参数值有两个，那么最后的图可能是这样的：
我们去掉J轴，用地理学中等高线的概念的表示上面的三维图，等高线的高度从外圈向内圈递减，同一条线的上J轴值相等如下右图所示：
在这两个参数所建立的二维坐标系中，每确定一组参数值，将有对应的J轴值，由图可知，J轴的最小值是最小圆的中心点。。
对于更多为的参数，我们无法画出这样的图形进行人工筛选求解，会通过梯段算法或者牛顿方法进行求解
假设我们有一个房价问题
给定的样本数据如图所示，现在需要根据这些点拟合出一个线性函数，以便于进行房价预测。
将样本数据进行整理如下:
m表示样本个数，x表示输入值，y表示输入出值。
使用
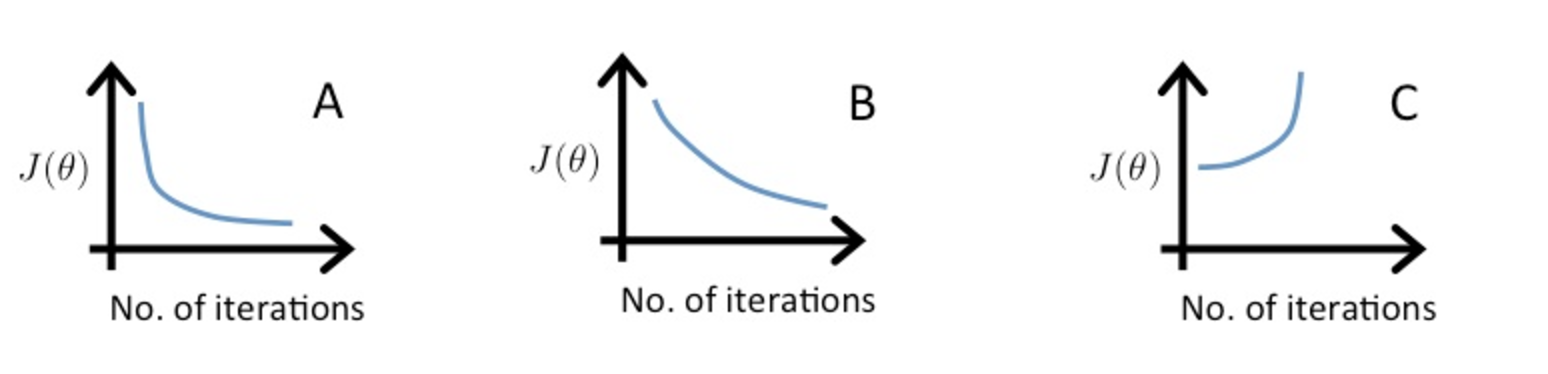
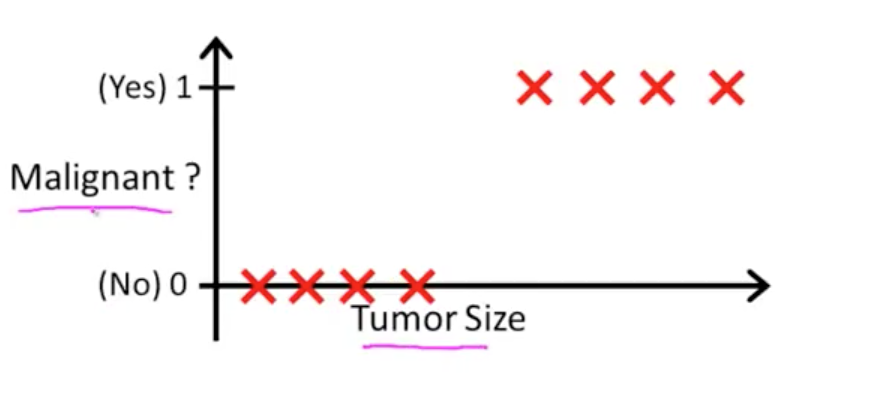
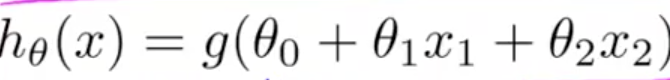
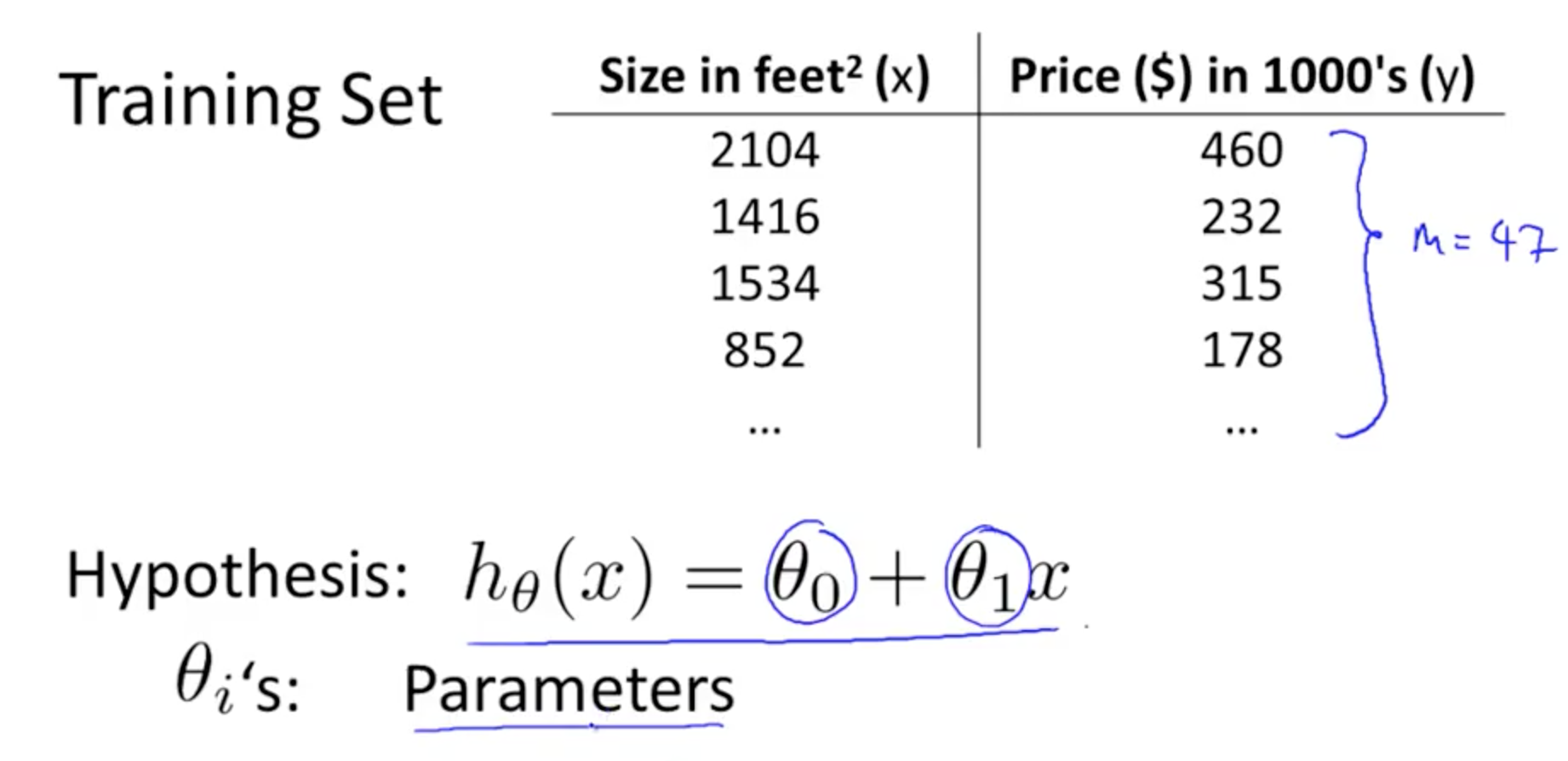
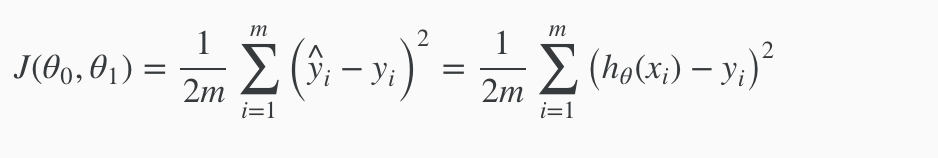
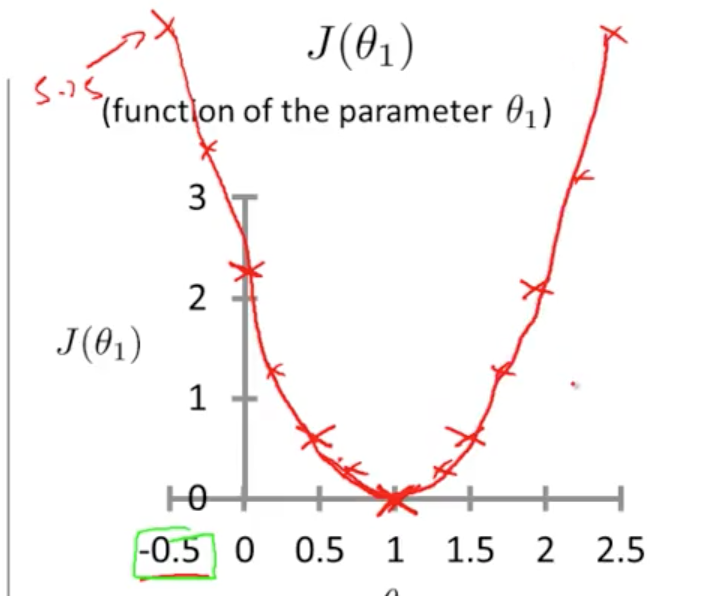
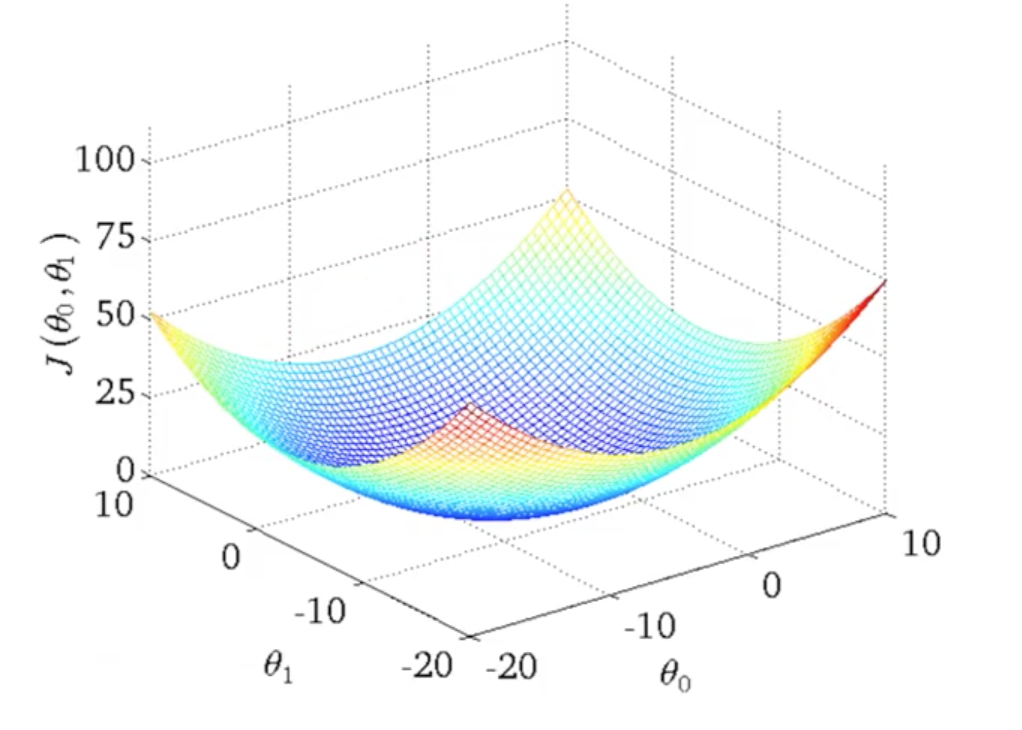
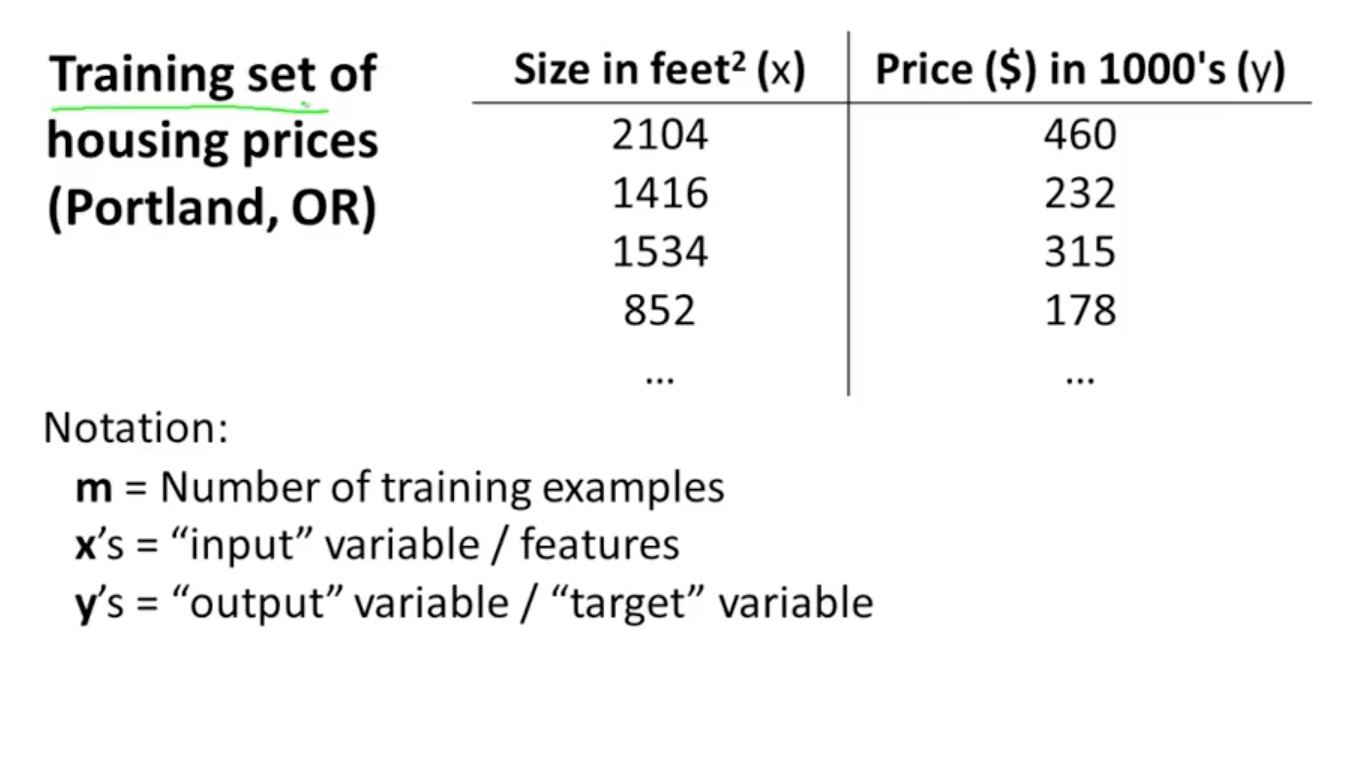
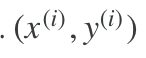表示样本第i行样本数据。
我们通过如如样本数据给学习算法，确定学习算法的参数值后得到学习算法，然后使用学习算法进行输出值的预测。
本讲讲解梯度下降。
问题：对于关于参数的函数J，求解参数值是的J的取值最小
主要思想：先任意设置参数初始值，通过不断迭代逐步使得J的取值达到最小，直到小于我们设定的阈值。
形象的说法：我们将函数平面看成是地形图，我们任意的站在山坡，希冀能以最快到速度跑到山底，那么选择什么方向最快呢，当然是
最陡峭的方向最快，这样在固定步长下，每步都选择最陡峭的方向往下走，当然可以最快跑到山底。这就是梯度下降原理的形象比喻，其中“最陡峭的方向”
在函数中即是函数在该点的梯度方向，通过梯度下降，总能找到局部最低点，并且不同的初始值可能会影响最终的最低点。
具体公式表达如下：
上图的参数更新方式注意两点：一是参数值是多个的情况下，每步迭代需要对每个参数进行梯度求导和计算
二是正确的参数迭代过程应当如上左图所示，右图的参数更新方式会将前一个已经更新的参数代入未更新的参数中进行更新，这会产生微小的错误。
方向导数前的系数疏于上叫做学习速率，学习速率太小会导致迭代次数多，学习速率太大，有可能会错过最优点。
随着梯度下降算法的迭代，约接近最小值，每次迭代的该变量会越来越小，这是因为接近最小值是梯度方向越来越缓，当找到最小点是，该点的偏导数为0.
迭代逼近：
以上的梯度下降称为批梯度下降，“批”的概念体现在每次迭代都需要遍历全部的样本，对应的还有随机梯度下降，每次只用一个样本，但是精度上比前者低。
梯度下降求得最优解一般是局部最优解，当代价函数是凸函数时，求得的是全局最优解。
监督学习：算法的训练有训练集数据和测试集数据，并且数据集都要正确的实际答案，基于这些数据进行算法的建模，并用此模型对给定的输入值，预测输出。应用领域如股市预测，房价预测等。
无监督学习：给定一个数据即，没有人告诉你改如何处理，也不知道数据的类别，你需要依据这些数据进行建模，找出这些数据集中数据的关系，比如聚类。应用领域有客户分组，认知识别等。
内存泄露是个程序开发中经久不衰的话题，外行人看应用外观设计，内容组织方式,来判断程序做的怎样；内行人看打开开发软件，通过观察代码架构，质量以及内存变化来判断应用质量的高低。
因为移动端硬件设备自身的特点，内存较小，在内存的处理上尤为重要，优秀的内存处理能增加应用的流畅性，减少内存占用，提升性能，避免出现OOM异常或者是其他因对象释放而造成的程序崩溃。。
1.所有对象的强引用都已经不存在，但是对象仍在内存中
2.无用对象由于强引用没有及时释放，占用内存
#内存泄露几种常见情况
循环强引用是造成内存泄露的一种常见方式。无论是java还是swift,类都可以进行嵌套。内部类持有外部类的引用，可以直接访问外部类，这是优势，方便了方法的调用和值的传递，但也正是因为如此，内部类很容易造成内存泄露。当外部类持有内部类一个对象的强引用的时候，就会形成形成了循环强引用。类似的java中的匿名内部类和swift以及OC中的闭包都会捕获上下文对象的引用，当闭包的生命周期超过上下文对象应有的生命周期时就会发生暂时性的内存泄露，比如开启一个线程，在java中我们会使用一个Runnable对象，这个对象捕获了上下文对象的引用，，runnable对象不会结束，线程的任务就不结束，runnable对象对上下文对象的强引用就不会释放，上下文对象属于无用的对象就造成了内存泄露，闭包同理。如果上下文对象对runnale对象持有强引用，那么将形成循环强引用，彼此永远无法释放。
iOS和Android都是单线程模型，两个平台所使用的语言中都使用runloop方式来解决事件排队问题，Android使用handler机制来做事件排队或者切换线程执行任务，当发送runnalbe任务时会造成短时间的上下文对象的内存泄露，比如我进入一个acitity活动页面，在第一个生命周期方法中使用handler向主线程发送一个runnable任务延时十秒执行，我进入页面后立即退出，观察内存可以发现activity对象并没有立即被销毁，而是过了十秒之后，当然可能是十一秒，也可能是十五秒，因为java的垃圾回收机制并不是时时刻刻都在回收的。iOS使用performSelector方法实现同样的功能，同理selector方法也会造成短时间的上下文内存泄露。
本教程默认Mac已经安装Ruby环境，如果没有安装Ruby，请自行搜索。
如果电脑没有安装cocopods,打开终端输入以下命令：
$ sudo gem install cocoapods
如果由于网络原因无法下载cocopods，那么我建议你使用淘宝镜像下载，具体的方式请自行搜索，并非本文重点。
如果已经安装，那么我建议你将cocopods更新到最新稳定版本，命令与上面一样。
在拉取之前你必须确定你已经安装了cocopods。步骤如下