本讲讲解梯度下降。
问题:对于关于参数的函数J,求解参数值是的J的取值最小

主要思想:先任意设置参数初始值,通过不断迭代逐步使得J的取值达到最小,直到小于我们设定的阈值。
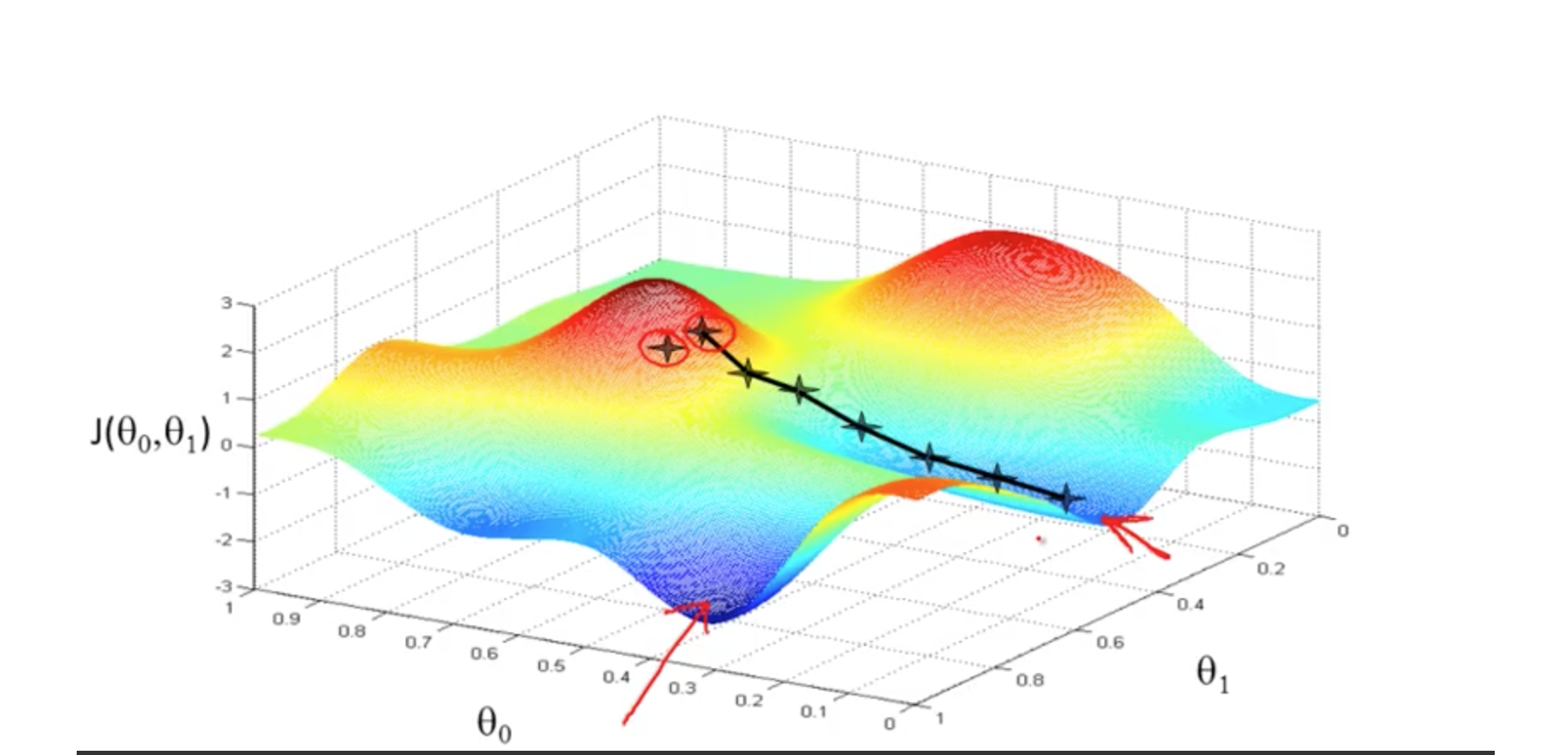
形象的说法:我们将函数平面看成是地形图,我们任意的站在山坡,希冀能以最快到速度跑到山底,那么选择什么方向最快呢,当然是
最陡峭的方向最快,这样在固定步长下,每步都选择最陡峭的方向往下走,当然可以最快跑到山底。这就是梯度下降原理的形象比喻,其中“最陡峭的方向”
在函数中即是函数在该点的梯度方向,通过梯度下降,总能找到局部最低点,并且不同的初始值可能会影响最终的最低点。
具体公式表达如下:

上图的参数更新方式注意两点:一是参数值是多个的情况下,每步迭代需要对每个参数进行梯度求导和计算
二是正确的参数迭代过程应当如上左图所示,右图的参数更新方式会将前一个已经更新的参数代入未更新的参数中进行更新,这会产生微小的错误。
方向导数前的系数疏于上叫做学习速率,学习速率太小会导致迭代次数多,学习速率太大,有可能会错过最优点。
随着梯度下降算法的迭代,约接近最小值,每次迭代的该变量会越来越小,这是因为接近最小值是梯度方向越来越缓,当找到最小点是,该点的偏导数为0.
迭代逼近:

以上的梯度下降称为批梯度下降,“批”的概念体现在每次迭代都需要遍历全部的样本,对应的还有随机梯度下降,每次只用一个样本,但是精度上比前者低。
梯度下降求得最优解一般是局部最优解,当代价函数是凸函数时,求得的是全局最优解。